What is an Octave? Wavelength, Frequency, and Harmonics Explained!

The musical interval of an octave can also be referred to as a Perfect Octave, or an eighth. It is fairly obvious that the word means 8 of something, so 8 whats?

It does not mean 8 steps, because it is really 7 steps away...specifically 5 whole steps and 2 half steps. If you are playing chromatically, then the octave is 12 half steps away. So, the 8 does not come from the number of notes you have to play to arrive at the right note, it really means "the 8th" note in a scale in which you count the starting note as "1" and the next note as "2", and so forth.

Have you ever noticed that there are only 7 letters used in the musical alphabet? A-G, right? So, if you start on "A" and think of it as "1", then count up through B, C, D, E, F, and G, then you have to use "A" again to get to "8". It doesn't matter whether you are using a major scale, minor scale, or any other type of scale. As long as you only use each letter once (with any combination of sharps or flats) you will arrive at the same letter that you started with for the 8th note.

This brings up an interesting question: Why is the octave so important that it caused early musicians to base the whole system of music theory on 7 note names? (Remember, 7 note names + 1 repeated note name = 8, or the octave) The answer is complicated, but I will give a somewhat simplified answer.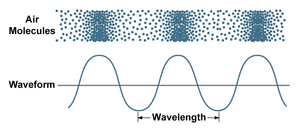

A musical tone can be measured in terms of its wavelength. Any sound causes a ripple or "wave" through the gaseous molecules that make up the air in our atmosphere. One molecule bumps into another, which bumps into another and so forth as the sound travels through the air. A musical tone, unlike other "sounds" or "noises" has a steady pulse of waves. Because the wave pulses are steady, they have a regular, exact, measurable distance between the start of one wave and the start of the next one. This is called the wavelength. When we graph a musical wave we draw a curvy line which goes up and down and up and down... We then show the wavelength as being the distance from one point on the "wave" to the correlating point on the next adjacent wave. Interestingly, the distance from the bottom of the wave to the top is used to show how LOUD a sound is (or the sound's amplitude).

---

Read More